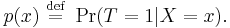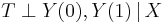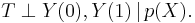Propensity score

In the design of experiments, a propensity score is the probability of a unit (e.g., person, classroom, school) being assigned to a particular condition in a study given a set of known covariates. Propensity scores are used to reduce selection bias by equating groups based on these covariates.

In the analysis of treatment effects, suppose that we have a binary treatment T, an outcome Y, and background variables X. The propensity score is defined as the conditional probability of treatment given background variables:

$p(x) \ \stackrel{\mathrm{def}}{=}\ \Pr(T=1 | X=x).$

The propensity score was introduced by Rosenbaum and Rubin (1983) to provide an alternative method for estimating treatment effects when treatment assignment is not random, but can be assumed to be unconfounded. Let Y(0) and Y(1) denote the potential outcomes under control and treatment, respectively. Then treatment assignment is (conditionally) unconfounded if treatment is independent of potential outcomes conditional on X. This can be written compactly as

$T \perp Y(0), Y(1) \,|\, X$

where $\perp$ denotes statistical independence.

Rosenbaum and Rubin showed that if unconfoundedness holds, then

$T \perp Y(0), Y(1) \,|\, p(X).$

Pearl (2000) has shown that a simple graphical criterion called backdoor provides an equivalent definition of unconfoundedness.

References

Pearl, J. (2000). Causality: Models, Reasoning, and Inference, Cambridge University Press.
Rosenbaum, P. R., and Rubin, D. B., (1983), "The Central Role of the Propensity Score in Observational Studies for Causal Effects," Biometrika 70, 41–55.

Propensity score

See also

References